Каждая фирма, взявшись за производство конкретного продукта, стремится добиться максимальной прибыли. Проблемы, связанные с производством продукции, могут быть разделены на три уровня:
- Перед предпринимателем может стоять вопрос о том, как производить заданное количество продукции на определенном предприятии. Эти проблемы относятся к вопросам краткосрочной минимизации издержек производства;
- предприниматель может решать вопросы о производстве оптимального, т.е. приносящего большую прибыль, количество продукции на определенном предприятии. Эти вопросы касаются долгосрочной максимизации прибыли;
- перед предпринимателем может стоять задача выяснения наиболее оптимальных размеров предприятия. Подобные вопросы относятся к долгосрочной максимизации прибыли.
Найти оптимальное решение можно на основе анализа взаимосвязи между издержками и объемом производства (выработкой). Ведь прибыль определяется разницей между выручкой от реализации продукции и всеми издержками. А выручка, и издержки зависят от объема производства. В качестве инструмента анализа этой зависимости экономическая теория использует производственную функцию.
Производственная функция определяет максимальный объем выпуска продукции при каждом заданном количестве ресурсов. Эта функция описывает зависимость между затратами ресурсов и выпуском продукции, позволяя определить максимально возможный объем выпуска продукции при каждом заданном количестве ресурсов, или минимально возможное количество ресурсов для обеспечения заданного объема выпуска продукции. Производственная функция суммирует только технологически эффективные приемы комбинирования ресурсов для обеспечения максимального выпуска продукции. Любое усовершенствование в технологии производства способствующее росту производительности труда, обусловливает новую производственную функцию.
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ – функция, отображающая зависимость между максимальным объемом производимого продукта и физическим объемом факторов производства при данном уровне технических знаний.
Поскольку объем производства зависит от объема использованных ресурсов, то зависимость между ними может быть выражена в виде следующей функциональной записи:
Q = f(L,K,M),
где Q – максимальный объем продукции, произведенной при данной технологии и определенных факторах производства;
L – труд; К – капитал; М – материалы; f – функция.
Производственная функция при данной технологии обладает свойствами, которые определяют соотношение между объемом производства и количеством используемых факторов. Для разных видов производства производственные функции различны, тем не менее? все они имеют общие свойства. Можно выделить два основных свойства.
- Существует предел для роста объема выпуска, который может быть достигнут ростом затрат одного ресурса при прочих равных условиях. Так, в фирме при фиксированном количестве машин и производственных помещений имеется предел роста выпуска путем увеличения дополнительных рабочих, поскольку рабочий не будет обеспечен машинами для работы.
- Существует определенная взаимная дополняемость (комплектарность) факторов производства, однако без уменьшения объема выпуска вероятна и определенная взаимозаменяемость данных факторов производства. Так, для выпуска блага могут быть использованы различные комбинации ресурсов; можно произвести это благо при использовании меньшего объема капитала и большего объема затрат труда, и наоборот. В первом случае производство считается технически эффективным в сравнении со вторым случаем. Однако существует предел того, насколько труд может быть заменен большим объемом капитала, чтобы не сократилось производство. С другой стороны, имеется предел применения ручного труда без использования машин.
В графической форме каждый вид производства может быть представлен точкой, координаты которой характеризуют минимально необходимые для выпуска данного объема продукции ресурсы, а производственная функция – линией изокванты.
Рассмотрев производственную функцию фирмы, перейдем к характеристике следующих трех важных понятий: общего (совокупного), среднего и предельного продукта.
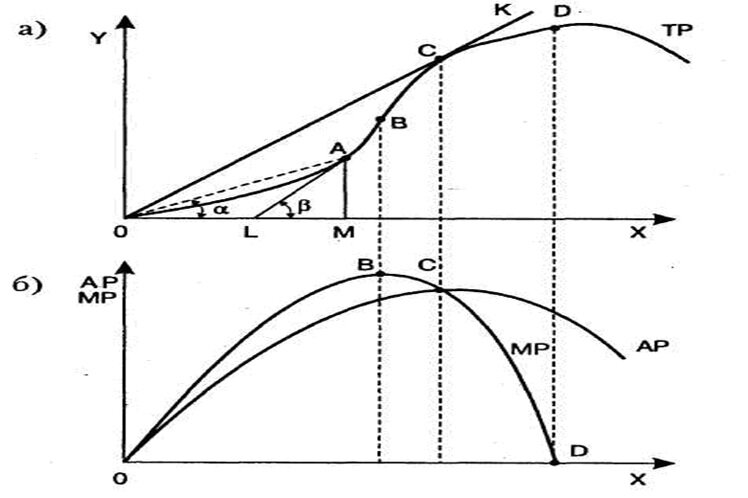
Рис. а) Кривая общего продукта (ТР); б) кривая среднего продукта (АР) и предельного продукта (МР)
На рис. показана кривая общего продукта (ТР), который изменяется в зависимости от величины переменного фактора X. На кривой ТР отмечены три точки: В – точка перегиба, С – точка, которая принадлежит касательной, совпадающей с линией, соединяющей данную точку с началом координат, D – точка максимального значения ТР. Точка А перемещается по кривой ТР. Соединив точку А с началом координат, получим линию ОА. Опустив перпендикуляр из точки А на ось абсцисс, получим треугольник ОАМ, где tg а есть отношение стороны AM к ОМ, т. е. выражение среднего продукта (АР).
Проведя через точку А касательную, получим угол Р, тангенс которого будет выражать предельный продукт МР. Сопоставляя треугольники LAM и ОАМ, находим, что до определенного момента тангенс Р по величине больше tg а. Таким образом, предельный продукт (МР) больше среднего продукта (АР). В том случае, когда точка А совпадает с точкой В, тангенс Р принимает максимальное значение и, следовательно, предельный продукт (МР) достигает наибольшего объема. Если точка А совпадает с точкой С, то значение среднего и предельного продукта равны. Предельный продукт (МР), достигнув максимального значения в точке В (рис. 22, б), начинает Сокращаться и в точке С пересечется с графиком среднего продукта (АР), который в этой точке достигает максимального значения. Затем и предельный, и средний продукт сокращаются, но предельный продукт уменьшается опережающими темпами. В точке максимума общего продукта (ТР) предельный продукт МР = 0.
Мы видим, что наиболее эффективное изменение переменного фактора X наблюдается на отрезке от точки В до точки С. Здесь предельный продукт (МР), достигнув своего максимального значения, начинает уменьшаться, средний продукт (АР) еще увеличивается, общий продукт (ТР) получает наибольший прирост.
Таким образом, производственная функция – это функция, позволяющая определить максимально возможный объем выпуска продукции при различных сочетаниях и количествах ресурсов.
В теории производства традиционно используются двухфакторная производственная функция, в которой объем производства, является функцией использования ресурсов труда и капитала:
Q = f (L, K).
Она может быть представлена в виде графика или кривой. В теории поведения производителей при определенных допущениях существует единственная комбинация ресурсов, при которой минимизируются затраты на ресурсы при данном объеме производства.
Расчет производственной функции фирмы – это поиск оптимума, выбор среди многих вариантов, предусматривающих различные сочетания факторов производства, такого, который даёт максимально возможный объем выпуска продукции. В условиях растущих цен и денежных затрат фирма, т.е. издержек на приобретение факторов производства, расчет производственной функции сосредоточен на поисках такого варианта, который обеспечил бы максимизацию прибыли при наименьших издержках.
Расчет производственной функции фирмы, стремящийся к достижению равновесия между предельными издержками и предельным доходом, будет сосредоточен на поиски такого варианта, который обеспечит необходимый выпуск продукции при минимальных издержках производства. Минимальные издержки определяются на стадии расчетов производственной функции методом замещения, вытеснения дорогостоящих или возросших в цене факторов производства альтернативными, более дешевыми. Замещение осуществляется с помощью сравнительного экономического анализа взаимозаменяемых и взаимодополняемых факторов производства их рыночных цен. Удовлетворительным будет такой вариант, в котором комбинация факторов производства и заданный объем выпуска продукции соответствует критерию наименьших издержек производства.
Существует несколько видов производственной функции. Основными из них являются:
- Нелинейная ПФ;
- Линейная ПФ;
- Мультипликативная ПФ;
- ПФ «затраты-выпуск».
Производственная функция и выбор оптимального размера производства
Производственная функция – это зависимость между набором факторов производства и максимально возможным объемом продукта, производимым с помощью данного набора факторов.
Производственная функция всегда конкретна, т.е. предназначается для данной технологии. Новая технология – новая производительная функция.
С помощью производственной функции определяется минимальное количество затрат, необходимых для производства данного объема продукта.
Производственные функции, независимо от того, какой вид производства ими выражается, обладают следующими общими свойствами:
- Увеличение объема производства за счет роста затрат только по одному ресурсу имеет предел (нельзя нанимать много рабочих в одно помещение – не у всех будут места).
- Факторы производства могут быть взаимодополняемы (рабочие и инструменты) и взаимозаменяемы (автоматизация производства).
В наиболее общем виде производственная функция выглядит следующим образом:
Q = f (K,L,M,T,N),
где L – объем выпуска;
K – капитал (оборудование);
М – сырье, материалы;
Т – технология;
N – предпринимательские способности.
Наиболее простой является двухфакторная модель производственной функции Кобба-Дугласа, с помощью которой раскрывается взаимосвязь труда (L) и капитала (К). Эти факторы взаимозаменяемы и взаимодополняемые
Q = AKα * Lβ,
где А – производственный коэффициент, показывающий пропорциональность всех функций и изменяется при изменении базовой технологии (через 30-40 лет);
K, L – капитал и труд;
α, β – коэффициенты эластичности объема производства по затратам капитала и труда.
Если = 0,25, то рост затрат капитала на 1% увеличивает объем производства на 0,25%.
На основе анализа коэффициентов эластичности в производственной функции Кобба-Дугласа можно выделить:
- пропорционально возрастающую производственную функцию, когда α + β = 1 (Q = K0,5 * L0,2).
- непропорционально – возрастающую α + β > 1 (Q = K0,9 * L0,8);
- убывающую α + β < 1 (Q = K0,4 * L0,2).
Оптимальные размеры предприятий не абсолютны по своей природе, а поэтому не могут устанавливаться вне времени и вне района размещения, так как они различны для разных периодов и экономических районов.
Оптимальный размер проектируемого предприятия должен обеспечить минимум затрат ли максимум прибыли, рассчитанных по формулам:
Тс+С+Тп+К*Ен_ – минимум, П – максимум,
где Тс – затраты на доставку сырья и материалов;
С – затраты на производство, т.е. себестоимость продукции;
Тп – затраты на доставку готовой продукции до потребителей;
К – капитальные затраты;
Ен – нормативный коэффициент эффективности;
П – прибыль предприятия.
Сл., под оптимальными размерами предприятий понимаются такие, которые обеспечивают выполнение заданий плана по выпуску продукции и приросту производственных мощностей с минусом приведенных затрат (с учетом капитальных вложений в сопряженные отрасли) и максимально возможной народнохозяйственной эффективностью.
Проблема оптимизации производства и соответственно ответа на вопрос, каким должен быть оптимальный размер предприятия, со всей остротой встала и перед западными предпринимателями, президентами компаний и фирм.
Те же, кому не удалось достичь необходимых масштабов, оказались в незавидном положении производителей с высокими издержками, обреченных на существование на грани разорения и в конечном счете банкротства.
Однако сегодня те американские компании, которые все еще стремятся преуспеть в конкурентной борьбе за счет экономии на концентрации производства, не столько выигрывают, сколько теряют. В современных условиях такой подход изначально ведет к снижению не только гибкости, но и эффективности производства.
Кроме этого, предприниматели помнят: небольшой размер предприятий означает меньший объем инвестиций и, следовательно, меньший финансовый риск. Что касается чисто управленческой стороны проблемы, то американские исследователи отмечают, что предприятия с числом занятых более 500 человек становятся плохо управляемыми, неповоротливыми и слабо реагируют на возникающие проблемы.
Поэтому ряд американских компаний в 60-е годы пошел на разукрупнение своих отделений и предприятий с целью существенного уменьшения размеров первичных производственных звеньев.
Помимо простого механического разукрупнения предприятий, организаторы производства проводят радикальную реорганизацию внутри предприятий, формируя в них командные и бригадные орг. структуры взамен линейно-функциональных.
При определении оптимального размера предприятия фирмы пользуются концепцией минимального эффективного размера. Он представляет собой просто наименьший объем производства, при котором фирма может минимизировать свои долгосрочные средние издержки.
Производственная функция и выбор оптимального размера производства.
Производством называется любая человеческая деятельность по преобразованию ограниченных ресурсов — материальных, трудовых, природных — в готовую продукцию. Производственная функция характеризует зависимость между количеством используемых ресурсов (факторов производства) и максимально возможным объемом выпуска, который может быть достигнут при условии, что все имеющиеся ресурсы используются наиболее рациональным образом.
Производственная функция обладает следующими свойствами:
- Существует предел увеличения производства, который может быть достигнут при увеличении одного ресурса и постоянстве прочих ресурсов. Если, например, в сельском хозяйстве увеличивать количество труда при постоянных количествах капитала и земли, то рано или поздно наступает момент, когда выпуск перестает расти.
- Ресурсы дополняют друг друга, но в определенных пределах возможна и их взаимозаменяемость без сокращения выпуска. Ручной труд, например, может заменяться использованием большего количества машин, и наоборот.
- Чем длиннее временной период, тем большее количество ресурсов может быть пересмотрено. В этой связи различают мгновенный, короткий и длительный периоды. Мгновенный период — период, когда все ресурсы являются фиксированными. Короткий период — период, когда, по крайней мере, один ресурс является фиксированным. Длительный период – период, когда все ресурсы являются переменными.
Обычно в микроэкономике анализируется двухфакторная производственная функция, отражающая зависимость выпуска (q) от количества используемых труда (L) и капитала (K). Напомним, что под капиталом понимаются средства производства, т.е. количество машин и оборудования, используемое в производстве и измеряемое в машино-часах. В свою очередь количество труда измеряется в человеко-часах.
Как правило, рассматриваемая производственная функция выглядит так:
q = AKαLβ
A, α, β — заданные параметры. Параметр А — это коэффициент совокупной производительности факторов производства. Он отражает влияние технического прогресса на производство: если производитель внедряет передовые технологии, величина А возрастает, т. е. выпуск увеличивается при прежних количествах труда и капитала. Параметры α и β — это коэффициенты эластичности выпуска соответственно по капиталу и труду. Иными словами, они показывают, на сколько процентов изменяется выпуск при изменении капитала (труда) на один процент. Коэффициенты эти положительны, но меньше единицы. Последнее означает, что при росте труда при постоянном капитале (либо капитала при постоянном труде) на один процент производство возрастает в меньшей степени.
Построение изокванты
Приведенная производственная функция говорит о том, что производитель может заменять труд капиталом и капитал трудом, оставляя выпуск неизменным. Например, в сельском хозяйстве развитых стран труд является высокомеханизированным, т.е. на одного работника приходится много машин (капитала). Напротив, в развивающихся странах тот же объем производства достигается за счет большого количества труда при незначительном капитале. Это позволяет построить изокванту (рис. 8.1).
Изокванта (линия равного продукта) отражает все комбинации двух факторов производства (труда и капитала), при которых выпуск остается неизменным. На рис. 8.1 рядом с изоквантой проставлен соответствующий ей выпуск. Так, выпуск q1, достижим при использовании L1 труда и K1 капитала или с использованием L2 труда и K2 капитала.
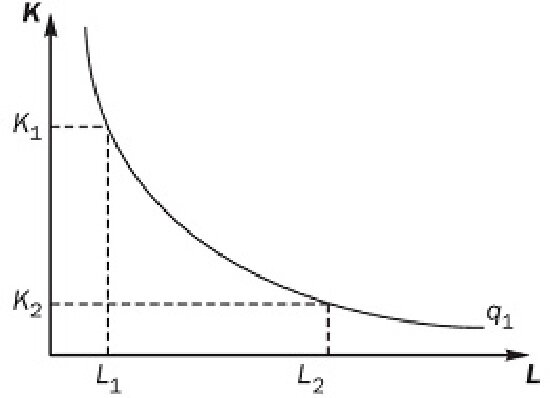
Рис. 8.1. Изокванта
Возможны и другие комбинации объемов труда и капитала, минимально необходимых для достижения данного выпуска.
Все комбинации ресурсов, соответствующих данной изокванте, отражают технически эффективные способы производства. Способ производства A является технически эффективным в сравнении со способом В, если он требует использования хотя бы одного ресурса в меньшем количестве, а всех остальных не в больших количествах в сравнении со способом В. Соответственно способ В является технически неэффективным в сравнении с А. Технически неэффективные способы производства не используются рациональными предпринимателями и не относятся к производственной функции.
Из вышесказанного вытекает, что изокванта не может иметь положительный наклон, как это показано на рис. 8.2.
Отрезок, выделенный пунктиром, отражает все технически неэффективные способы производства. В частности, в сравнении со способом А способ В для обеспечения одинакового выпуска (q1) требует того же количества капитала, но большего количества труда. Очевидно, поэтому, что способ B не является рациональным и не может приниматься в расчет.
На основе изокванты можно определить предельную норму технической замены.
Предельная норма технической замены фактора Y фактором X (MRTSXY) — это количество фактора Y (например, капитала), от которого можно отказаться при увеличении фактора X (например, труда) на 1 ед., чтобы выпуск не изменился (остаемся на прежней изокванте).
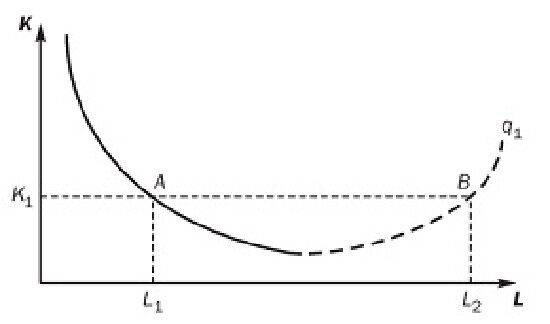
Рис. 8.2. Технически эффективное и неэффективное производство
Следовательно, предельная норма технической замены капитала трудом исчисляется по формуле
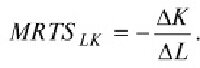 При бесконечно малых изменениях L и K она составляет
При бесконечно малых изменениях L и K она составляет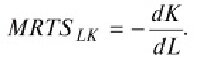
Таким образом, предельная норма технической замены есть производная функции изокванты в данной точке. Геометрически она представляет собой наклон изокванты (рис. 8.3).
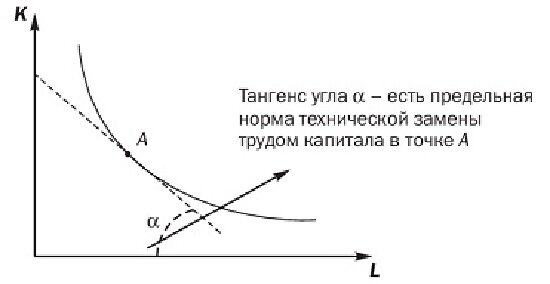
Рис. 8.3. Предельная норма технической замены
При движении сверху — вниз вдоль изокванты предельная норма технической замены все время убывает, о чем говорит уменьшающийся наклон изокванты.
Если же производитель увеличивает и труд, и капитал, то это позволяет ему достичь большего выпуска, т.е. перейти на более высокую изокванту (q2). Изокванта, расположенная правее и выше предыдущей, соответствует большему объему выпуска. Совокупность изоквант образует карту изоквант (рис. 8.4).
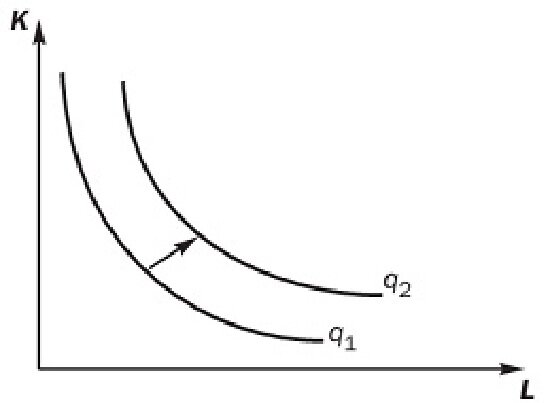
Рис. 8.4. Карта изоквант
Особые случаи изоквант
Напомним, что приведенные изокванты соответствуют производственной функции вида q = AKαLβ. Но бывают и другие производственные функции. Рассмотрим случай, когда имеет место совершенная замещаемость факторов производства. Допустим, например, что на складских работах можно использовать квалифицированных и неквалифицированных грузчиков, причем производительность квалифицированного грузчика в N раз выше, чем неквалифицированного. Это означает, что мы можем заменить любое количество квалифицированных грузчиков неквалифицированными в соотношении N к одному. И наоборот, можно заменить N неквалифицированных грузчиков одним квалифицированным.
Производственная функция при этом имеет вид: q = ax + by, где x — число квалифицированных рабочих, y — число неквалифицированных рабочих, а и b — постоянные параметры, отражающие производительность соответственно одного квалифицированного и одного неквалифицированного рабочего. Соотношение коэффициентов а и b — предельная норма технической замены неквалифицированных грузчиков квалифицированными. Она постоянна и равна N: MRTSxy = a/b = N.
Пусть, например, квалифицированный грузчик в состоянии в единицу времени обработать 3 т груза (это будет коэффициент а в производственной функции), а неквалифицированный — только 1 т (коэффициент b). Значит, работодатель может отказаться от трех неквалифицированных грузчиков, дополнительно нанимая одного квалифицированного грузчика, чтобы выпуск (общий вес обработанного груза) при этом остался прежним.
Изокванта в данном случае является линейной (рис. 8.5).
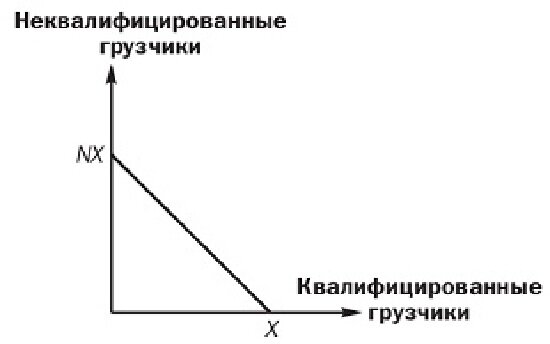
Рис. 8.5. Изокванта при совершенной заменяемости факторов
Тангенс угла наклона изокванты равен предельной норме технической замены неквалифицированных грузчиков квалифицированными.
Еще одна производственная функция — функция Леонтьева. Она предполагает жесткую дополняемость факторов производства. Это означает, что факторы могут использоваться только в строго определенной пропорции, нарушение которой технологически невозможно. Например, авиационный рейс может быть нормально осуществлен при наличии как минимум одного самолета и пяти членов экипажа. При этом нельзя увеличивать самолето-часы (капитал), одновременно сокращая человеко-часы (труд), и наоборот, и сохранять неизменным выпуск. Изокванты в данном случае имеют вид прямых углов, т.е. предельные нормы технической замены равны нулю (рис. 8.6). В то же время можно увеличивать выпуск (количество рейсов), увеличивая в одной и той же пропорции и труд, и капитал. Графически это означает переход на более высокую изокванту.
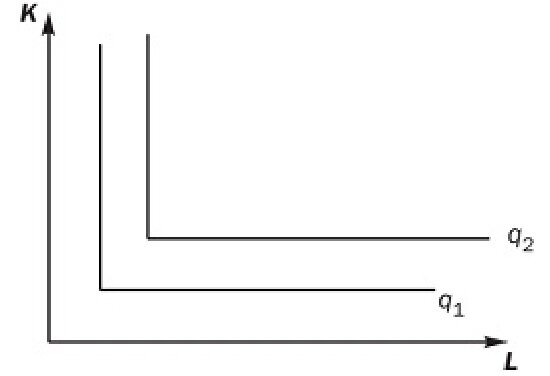
Рис. 8.6. Изокванты в случае жесткой дополняемости факторов производства
Аналитически такая производственная функция имеет вид: q = min {aK; bL}, где а и b — постоянные коэффициенты, отражающие производительность соответственно капитала и труда. Соотношение этих коэффициентов определяет пропорцию использования капитала и труда.
В нашем примере с авиарейсом производственная функция выглядит так: q = min{1K; 0,2L}. Дело в том, что производительность капитала здесь составляет один рейс на один самолет, а производительность труда — один рейс на пять человек или 0,2 рейса на одного человека. Если авиакомпания располагает самолетным парком в 10 машин и имеет 40 человек летного персонала, то ее максимальный выпуск составит: q = min{ 1 х 8; 0,2 х 40} = 8 рейсов. Два самолета при этом будут простаивать на земле из-за нехватки персонала.
Взглянем, наконец, на производственную функцию, предполагающую существование ограниченного числа производственных технологий для производства заданного количества продукции. Каждой из них соответствует определенное состояние труда и капитала. В результате мы имеем ряд опорных точек в пространстве «труд-капитал», соединив которые, получаем ломаную изокванту (рис. 8.7).
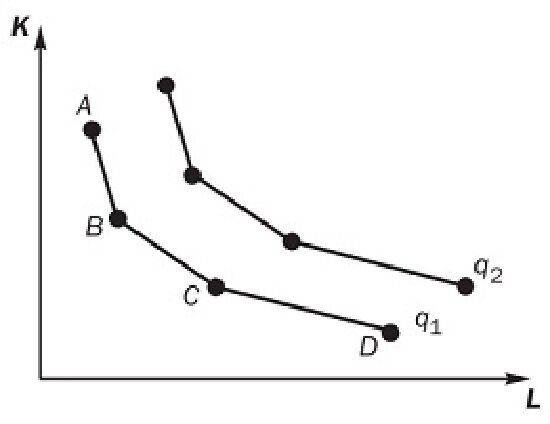
Рис. 8.7. Ломаные изокванты при наличии ограниченного числа производственных методов
На рисунке видно, что выпуск продукции в объеме q1 можно получить при четырех комбинациях труда и капитала, соответствующих точкам А, B, С и D. Возможны также и промежуточные комбинации, достижимые в тех случаях, когда предприятие совместно использует две технологии для получения определенного совокупного выпуска. Как всегда, увеличив количества труда и капитала, мы переходим на более высокую изокванту.
